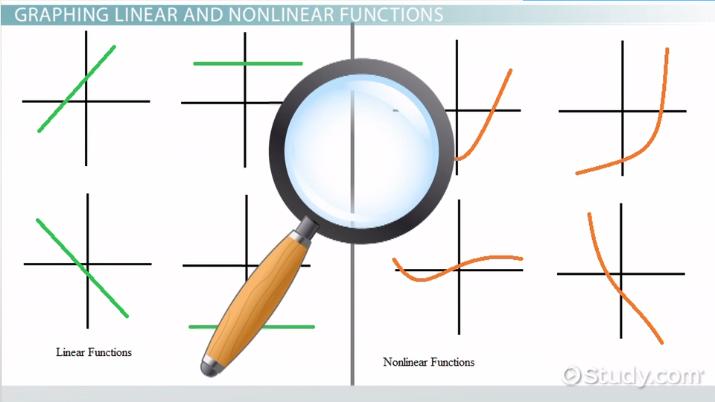
Fungsi linear dengan nama lain Persamaan Garis Lurus (PGL) adalah salah satu sub bidang di mata pelajaran matematika yang pasti kamu pelajari saat mengenyam bangku sekolah, tepatnya saat SMA. PGL bisa diterapkan dalam berbagai sektor kehidupan, lo, salah satunya di bidang ekonomi. Simak bahasan ringkasnya berikut ini, yuk!
Pengertian Fungsi dalam Matematika
Istilah fungsi linear atau persamaan garis lurus berakar dari dua kata – fungsi dan linear. Tapi, apa itu sebenarnya fungsi dari kacamata Matematika?
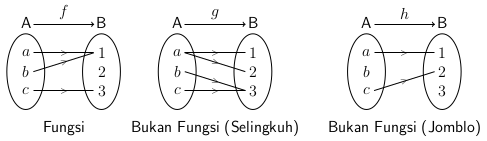
Fungsi bisa diartikan sebagai konsep yang menghubungkan setiap anggota pada dua himpunan. Sederhananya, sub bidang pada mata pelajaran matematika ini akan menghubungkan setiap anggota pada himpunan (A) dengan setiap anggota pada himpunan (B).
Semua anggota pada himpunan (A) harus punya pasangan dari himpunan (B). Namun, jika ada himpunan (B) yang tidak dapat pasangan dari himpunan (A), itu bukanlah masalah.
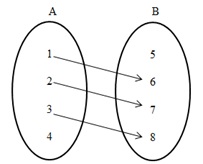
Satu hal lagi yang perlu kamu ingat adalah bahwa jumlah pasangan semua anggota himpunan (A) pada himpunan (B) masing-masing hanya satu. Jadi, jika ada anggota dari himpunan (A) yang punya lebih dari satu pasangan, itu bukanlah fungsi.
Bagaimana dengan himpunan (B)? Nah, kalau himpunan (B) mendapatkan pasangan lebih dari satu di himpunan (A), tidak masalah.
Kalau kamu ingat-ingat kembali, persamaan garis lurus pasti tidak lepas dari tiga istilah ini, yaitu variabel, konstanta, dan koefisien.
Apa Itu Fungsi Linear?
Sebelumnya kita sudah membahas secara singkat apa itu fungsi. Nah, lalu, apa itu fungsi linear atau persamaan garis lurus?
Simpelnya, persamaan garis lurus adalah suatu fungsi yang akan membentuk garis lurus. Selain itu, pangkat tertinggi variabel pada pada persamaan garis lurus adalah sama dengan satu.
Di bawah ini kamu bisa lihat contoh dari persamaan garis lurus.
Sempat kita bahas di awal kalau konsep persamaan garis lurus sangat bisa diterapkan dalam kehidupan nyata. Konsep ini sering kali digunakan oleh para ekonom dan pebisnis dalam memecahkan dan menganalisis berbagai masalah yang berkaitan dengan ekonomi.
Jadi, segala kebijakan ekonomi yang sering kamu temui, juga prediksi ekonomi di masa depan yang sering kamu dengar dari ahli ekonomi itu bukanlah tanpa dasar. Pasalnya, mereka juga memanfaatkan fungsi linear sebagai salah satu pendekatan dalam menganalisis aspek-aspek terkait.
Itulah sebabnya, pemahaman dan penerapan PGL menjadi penting.
Baca Juga : Pertidaksamaan Linear: Pengertian, Sistem, Bentuk Umum, Contoh
Rumus Fungsi Linear
Supaya kamu paham cara kerja persamaan garis lurus, kamu perlu melihat rumusnya. Berikut ini adalah bentuk umumnya.
f : x → ax + b
Atau, dalam notasi fungsi umum adalah
f(x) = ax + b
y = ax + b
Dengan begitu, kalau kita menggunakan konsep kemiringan garis (gradien), koefisien (a) dapat kita ganti dengan koefisien kemiringan – atau kita tandai sebagai (m).
f(x) = mx + b
y = mx + b
Keterangan:
- m = kemiringan atau gradien,
- c = konstanta.
Kalau (m) menggambarkan kemiringan suatu garis, bagaimana dengan kode (c) atau konstanta?
Konstanta atau yang dilambangkan dengan (c) menggambarkan titik potong suatu garis terhadap sumbu (y).
Jika kita belajar tentang fungsi linear, tentu kita pasti akan menggambar grafik, sehingga kamu harus memperhatikan beberapa unsur berikut agar dapat menggambar grafik dengan benar.
- Di manapun letak titik potong terhadap sumbu (x), sudah pasti y = 0, dengan koordinat (x,0).
- Di manapun letak titik potong terhadap sumbu (y), sudah pasti x = 0, dan koordinat (0,y).
- Dua titik (A dan B) jika kamu hubungkan akan membentuk sebuah garis lurus dengan persamaan y = mx + b.
- Jika (b) bernilai positif, sebuah garis akan digambar dari arah kiri bawah ke kanan atas.
- Jika (b) bernilai negatif maka, sebuah garis akan digambar dari kiri atas ke kanan bawah.
- Sedangkan, jika (b) nilainya 0 maka, sebuah garis akan digambar sejajar dengan sumbu (x).
Contoh Soal Persamaan Linear dan Pembahasannya
Nah, sekarang kita masuk ke bagian yang paling kamu tunggu-tunggu – contoh soal persamaan linear dan pembahasan lengkapnya.
Beberapa contoh soal beserta pembahasannya ini akan membantumu untuk memahami prinsip persamaan garis lurus dengan cepat dan mudah.
Contoh Soal 1
Suatu fungsi linear diketahui sebagai berikut f(x) = 3x + b. Tentukan bentuk fungsi tersebut jika diketahui f(5) = 18.
Pembahasan
f(x) = 3x + b
f(5) = 3(5) + b = 18
15 + b = 18
b = 18-15
b = 3
Jadi, bentuk fungsinya adalah f(x) = 3x + 3
Contoh Soal 2
Terdapat suatu fungsi linear yaitu f(x) = 7x + b. Tentukan bentuk fungsi linier tersebut jika diketahui f(3) = 25.
Pembahasan
f(x) = 7x + b
f(3) = 7(3) + b = 25
21 + b = 25
b = 25-21
b = 4
Jadi, bentuk fungsinya adalah f(x) = 7x + 4
Contoh Soal 3
Layanan parkir di sebuah pusat perbelanjaan menetapkan tarif parkir awal sebesar Rp2.000 untuk sepeda motor. Lalu, biaya parkir selanjutnya diteruskan sebesar Rp1.000 per jam.
Budi mulai memarkir sepeda motornya di tempat parkir pusat perbelanjaan pada pukul 10.00 WIB dan mengambil kembali motornya pada pukul 18.00 WIB.
Berapakah biaya parkir yang harus Budi bayar?
Pembahasan
Kita membuat permisalan yaitu.
Tarif parkir sepeda motor = f(x)
Tarif parkir sepeda motor per jam = x
Maka,
x = pukul 11.00 WIB ke 18.00 WIB = 7 jam
x = 7
f(x) = 1.000x + 2.000
f(7) = 1.000(7) + 2.000
f(7) = 7.000 + 2.000
Jadi, f(7) = Rp9.000
Jadi, biaya parkir sepeda motor total yang harus Budi bayar dari jam 11.00 hingga jam 18.00 adalah Rp9.000.
Contoh Soal 4
Terdapat suatu fungsi linear yaitu f(x) = 4x + b. Tentukan bentuk fungsi linier tersebut jika diketahui f(10) = 48.
Pembahasan
f(x) = 4x + b
f(10) = 4(10) + b = 48
40 + b = 48
b = 48-40
b = 8
Jadi, bentuk fungsinya adalah f(x) = 4x + 8
Contoh Soal 5
Sebuah warnet menetapkan tarif awal untuk menyewa komputer sebesar Rp10.000. Selanjutnya, biaya sewa komputer selanjutnya akan dikenakan biaya sebesar Rp7.000 per jam. Ucok ingin menyewa komputer dari jam 12.00 WIB hingga pukul 20.00 WIB untuk mengerjakan tugas makalah.
Berapa biaya sewa komputer yang harus Ucok bayar ke pihak warnet?
Pembahasan
Kita membuat permisalan yaitu.
Tarif sewa komputer di warnet = f(x)
Tarif sewa komputer per jam = x
Maka,
x = pukul 12.00 WIB ke 20.00 WIB = 8 jam
x = 8
f(x) = 7.000x + 10.000
f(8) = 7.000(8) + 10.000
f(8) = 56.000 + 10.000
Jadi, f(8) = Rp66.000
Jadi, biaya sewa komputer total yang harus Ucok bayar ke pihak warnet setelah menyewa dari jam 12.00 hingga jam 20.00 adalah Rp66.000.
Contoh Soal 6
Terdapat suatu fungsi linear yaitu f(x) = 5x + b. Tentukan bentuk fungsi linier tersebut jika diketahui f(5) = 30.
Pembahasan
f(x) = 5x + b
f(5) = 5(5) + b = 30
25 + b = 30
b = 30-25
b = 5
Jadi, bentuk fungsinya adalah f(x) = 5x + 5
Baca Juga : Persamaan Linear Dua Variabel: Metode Grafik dan Substitusi
Memahami Fungsi Linear Itu Mudah, Bukan?
Persamaan garis lurus adalah salah satu konsep ilmu dari mata pelajaran Matematika yang biasanya kamu pelajari di bangku SMA. Persamaan garis lurus tidak terlepas dari tentang variabel, konstanta dan koefisien. Di samping itu, konsep ini juga berkaitan dengan penggambaran grafik.
Oleh sebab itu, kamu perlu memahami dan menghapal enam unsur penting terkait penggambaran grafik untuk konsep PGL.
Fungsi linear dapat diterapkan dalam berbagai analisis di kehidupan nyata, seperti yang para pebisnis dan ekonom lakukan di sektor ekonomi. Bahkan, konsep ini dapat memudahkan kamu melakukan berbagai perhitungan untuk berbagai kasus sederhana dalam kehidupan, seperti pada contoh soal nomor 3 dan 5 di atas.