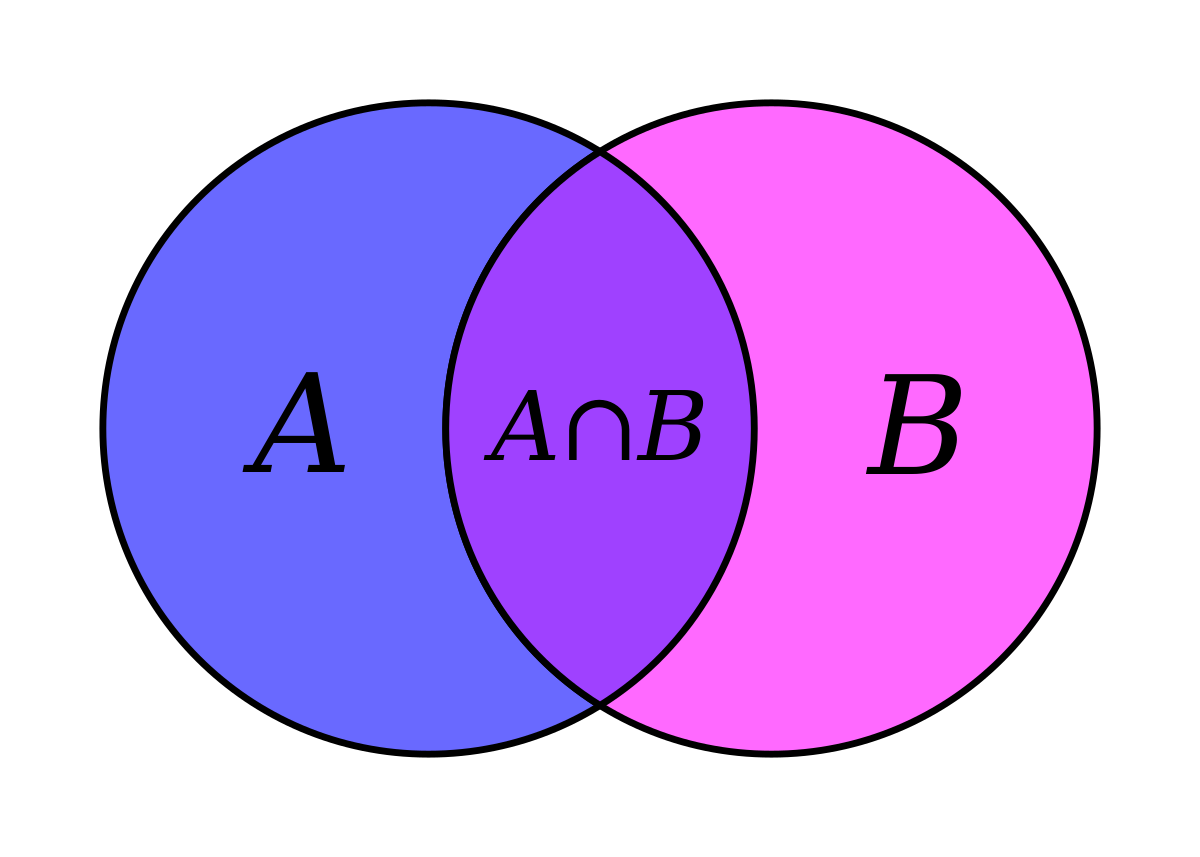
Dalam matematika, irisan himpunan adalah salah satu operasi dasar yang berguna untuk memahami hubungan antara himpunan-himpunan. Konsep ini juga dapat digunakan untuk berbagai masalah dalam bidang ilmu lain, seperti statistik, ilmu komputer, ilmu sosial, dan banyak bidang lainnya.
Oleh karena itu, mari kenali lebih dalam terkait dengan irisan himpunan beserta dengan contoh dan pembahasannya melalui artikel berikut. Baca sampai selesai, ya!
Apa Itu Irisan Himpunan?
Irisan atau intersection antara dua himpunan adalah himpunan yang terdiri dari semua elemen atau anggota dari himpunan satu yang juga milik himpunan lainnya. Biasanya, intersection dari dua himpunan atau set ini memiliki simbol umum yakni ∩.
Misalnya, jika A dan B adalah dua himpunan yang berbeda, maka irisan himpunan A dan B adalah A ∩ B. Sebab, masing-masing himpunan A dan B memiliki beberapa elemen yang sama sehingga A ∩ B akan berisi himpunan elemen yang ada pada A dan B pada saat yang sama.
Konsep operasi ini banyak digunakan dalam pemecahan masalah matematika atau analisis data untuk mengidentifikasi persamaan atau kesamaan antara dua kelompok data yang berbeda.
Pemahaman tentang irisan himpunan sangat berguna dalam aktivitas pengolahan data, analisis statistik, pemodelan matematika, dan berbagai aplikasi lainnya yang mana perlu mengidentifikasi elemen-elemen bersama dari himpunan-himpunan yang berbeda.
Adapun dalam teori himpunan, intersection adalah salah satu operasi dasar yang berguna untuk menghasilkan beberapa himpunan baru, seperti gabungan, perbedaan, atau komplemen.
Cara Menentukan Irisan Himpunan

Menentukan intersection dari dua atau lebih himpunan relatif mudah, tergantung pada isi dan jumlah dari masing-masing himpunan. Untuk menentukan intersection antara dua himpunan, Anda dapat mengikuti langkah-langkah mudahnya sebagai berikut:
- Pertama, identifikasi dua himpunan yang ingin Anda cari irisannya. Misalnya, ketika Anda memiliki himpunan A dan himpunan B.
- Langkah selanjutnya adalah Anda dapat menuliskan himpunan tersebut dalam bentuk daftar elemen-elemen. Sebagai contoh, himpunan A adalah {1, 2, 3, 4, 5} dan himpunan B adalah {3, 4, 5, 6, 7}.
- Kemudian, Anda dapat menggunakan simbol irisan (∩) untuk mengekspresikan operasi atau konsep ini antara himpunan-himpunan tersebut.
- Nantinya, Anda dapat mengidentifikasi elemen-elemen yang ada dalam kedua himpunan tersebut.
- Terakhir, Anda dapat menulis hasil operasi sebagai himpunan baru yang berisi elemen-elemen tersebut. Dalam contoh di atas, hasil dari irisan A dan B adalah A ∩ B = {3, 4, 5}.
Dengan mengikuti langkah-langkah di atas, Anda dapat menentukan irisan himpunan dengan mudah. Langkah-langkah tersebut adalah cara paling umum yang dapat Anda gunakan untuk menjalankan operasi-operasi matematika dalam teori himpunan.
Dalam hal ini, Anda juga harus memahami penulisan intersection dalam suatu himpunan. Adapun penulisan notasi intersection untuk himpunan A dan B adalah A n B = {x | x ∈ A dan x ∈ B}.
Baca Juga : Definisi Himpunan, Cara Menyatakan, Jenis, dan Contoh Soalnya
Contoh Soal Irisan Himpunan dan Pembahasannya
Cara menghitung irisan himpunan adalah dengan memasukkan semua elemen yang ada dalam kedua himpunan tersebut ke dalam irisan. Contoh sederhana dari operasi ini adalah sebagai berikut:
Misalkan A = {5, 6, 7, 8} dan B = {7, 8, 9, 10}. Maka irisan himpunan A dan B adalah:
A ∩ B = {7, 8}
Maksudnya, irisan himpunan A dan B adalah himpunan {7, 8}, yang mana merupakan elemen-elemen yang ada dalam kedua himpunan A dan B. Dalam konteks ini, irisan himpunan berperan sebagai alat untuk menganalisis kesamaan atau persamaan antara dua himpunan data A dan B.
Untuk memahami operasi ini dengan lebih dalam, Anda dapat menyimak contoh soal berikut ini untuk melatih pemahaman terkait himpunan:
1. Contoh Soal 1
Dikutahui terdapat tiga himpunan yang berbeda yakni A, B, dan C dengan masing-masing nilai sebagai berikut:
- Himpunan A = {2, 4, 6, 8, 10}
- Himpunan B = {3, 6, 9, 12, 15}
- Himpunan C = {6, 12, 18, 24, 30}
Hitunglah ketiga irisan tersebut!
Pembahasan:
Untuk menghitung operasi dasar interseksi A, B, dan C, Anda perlu mencari elemen-elemen yang ada dalam ketiga himpunan tersebut. Identifikasi elemen-elemen yang ada dalam himpunan A, B, dan C adalah sebagai berikut.
A = {2, 4, 6, 8, 10}
B = {3, 6, 9, 12, 15}
C = {6, 12, 18, 24, 30}
Setelah itu, Anda dapat mulai menentukan irisan himpunan A dan B terlebih dahulu:
A ∩ B = {6}
Selanjutnya, Anda dapat mencari interseksi antara hasil A ∩ B dengan himpunan C:
(A ∩ B) ∩ C = {6} ∩ {6, 12, 18, 24, 30}
Sehingga, Anda akan menemukan irisan kedua set tersebut seperti berikut:
{6} ∩ {6, 12, 18, 24, 30} = {6}
Jadi, hasil dari A, B, dan C adalah {6}. Ini adalah elemen yang sama dan ada dalam ketiga himpunan yakni A, B, dan C atau A ∩ B ∩ C.
2. Contoh Soal 2
Diketahui terdapat tiga himpunan yang berbeda yakni O, P, dan Q. Cari dan hitunglah intersection dari ketiga himpunan tersebut:
- Himpunan O = {2, 5, 6, 10, 11}
- Himpunan P = {3, 6, 9, 12}
- Himpunan Q = {4, 8, 12}
Pembahasan:
Pertama-tama, Anda dapat menghitung irisan himpunan antara O dan P, yaitu (O ∩ P). Kemudian, Anda lanjutkan hitung hasil intersection tersebut dengan himpunan Q, yaitu ((O ∩ P) ∩ Q).
Langkah pertama adalah dengan menghitung O ∩ P. Himpunan O ∩ P adalah himpunan yang berisi elemen-elemen yang ada dalam kedua himpunan O dan P. Maka dalam hal ini, hasil O ∩ P adalah {6}.
Langkah kedua adalah dengan menghitung ((O ∩ P) ∩ Q). Himpunan ((O ∩ P) ∩ Q) adalah intersection antara hasil dari langkah pertama (O ∩ P) dengan himpunan Q. Maka, hasil dari ((A ∩ B) ∩ C) adalah ({6} ∩ {4, 8, 12}).
Sekarang, Anda dapat mencari elemen-elemen yang ada dalam kedua set tersebut. Dalam hal ini, ((A ∩ B) ∩ C) = { } atau himpunan kosong. Hasil himpunan ini bisa muncul ketika tidak ada elemen yang sama terdapat dalam hasil himpunan {6} dan himpunan {4, 8, 12}.
Jadi, dapat Anda simpulkan bahwa irisan himpunan (A ∩ B) ∩ C adalah himpunan kosong. Himpunan kosong adalah suatu himpunan yang tidak memiliki elemen sama sekali. Himpunan kosong memiliki lambang khusus dengan simbol ∅ atau {}.
Jadi, Sudah Tahu Apa Itu Irisan Himpunan?
Demikianlah pembahasan singkat apa itu irisan himpunan, cara menentukan, hingga contoh soal dan pembahasannya. Mempelajari operasi dasar irisan himpunan dengan teliti akan membantu Anda dalam memahami keseluruhan konsep himpunan dengan baik.
Kenali sifat-sifat irisan seperti komutatif, asosiatif, distributif, dan lainnya. Pemahaman ini akan membantu Anda dalam manipulasi himpunan-himpunan yang lebih kompleks. Bila perlu, kerjakan banyak contoh latihan untuk mengasah keterampilan Anda dalam menghitung irisan.