Rumus bangun ruang adalah salah satu pelajaran matematika yang wajib dipelajari ketika masih duduk di bangku sekolah. Ketika berbicara tentang bangun ruang, pasti yang terlintas di benak adalah kubus dan balok. Namun tidak hanya itu saja, bangun ruang memiliki beragam jenis seperti kerucut, bola, tabung, dan limas.
Lantas apa saja rumus bangun ruang? Simak artikel di bawah ini!
Pengertian Bangun Ruang
Secara sederhana, bangun ruang itu sendiri merupakan bangun dengan tiga dimensi yang memiliki volume atau isi. Terdapat tiga unsur tertentu pada bangun ruang, yaitu rusuk, titik sudut, dan bidang sisi.
Selain itu, bangun ruang memiliki berbagai jenis berdasarkan bentuk bidangnya. Jenis pertama yaitu bangun ruang bidang datar yang terdiri dari kubus, balok, limas, dan prisma. Sementara itu, jenis lainnya yaitu bangun ruang bidang lengkung yang meliputi 3 jenis bangun, yakni bola, kerucut, dan tabung.
6 Rumus Bangun Ruang: Volume dan Luas Permukaan
Berikut ini adalah rumus bangun ruang untuk mencari volume dan luas permukaan pada kubus, kerucut, dan limas.
1. Kubus
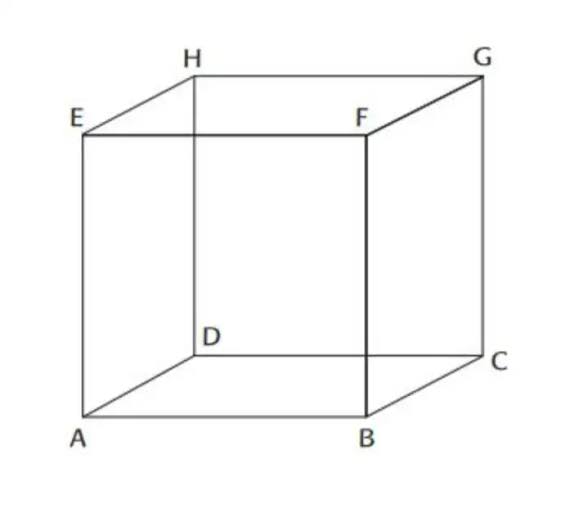
Kubus adalah bangun ruang tiga dimensi yang tersusun dari 6 sisi (s) berbentuk persegi dengan ukuran yang sama. Kubus juga termasuk ke dalam bangun ruang sisi datar yang mempunyai 8 titik sudut dan 12 rusuk dengan panjang yang sama.
Contoh dari kubus dalam kehidupan sehari-hari yaitu dadu, kardus, gula batu, blok lego, dan lain sebagainya. Adapun sifat-sifat kubus antara lain:
- Memiliki 6 sisi, 8 titik sudut, dan 12 rusuk sama panjang
- Sisi kubus berbentuk persegi
- Mempunyai 6 diagonal yang sama berbentuk persegi panjang
- Besar diagonal berbeda-beda
Rumus volume kubus tertulis seperti ini:
a. Volume Kubus
- V = s x s xs atau V = s3
Sedangkan rumus luas permukaan kubus yaitu dengan menambahkan semua luas pada masing-masing sisi. Rumusnya adalah:
b. Luas Permukaan Kubus
- L = 6 x (s x s)
Keterangan:
s = panjang rusuk atau sisi
V = Volume
L = Luas permukaan
2. Kerucut
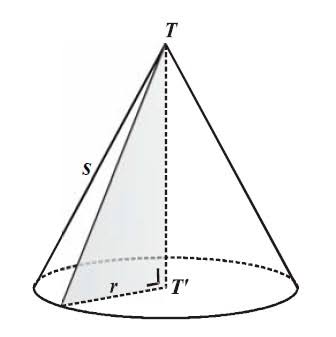
Rumus bangun ruang selanjutnya yaitu kerucut. Ini adalah bangun ruang tiga dimensi yang memiliki alas bundar dan sebuah bidang lengkung yang menjuntai ke atas. Kerucut hampir sama dengan tabung yang termasuk ke dalam bangun ruang sisi lengkung.
Adapun contoh kerucut dalam kehidupan sehari-hari yaitu topi ulang tahun, tutup saji, kukusan, cone ice cream, caping, dan lain sebagainya. Kerucut memiliki beberapa sifat, diantaranya:
- Memiliki 2 bidang sisi yang berbeda
- Satu sisi berbentuk lingkaran dan sisi lainnya berbentuk melengkung
- Tidak memiliki bidang diagonal
- Hanya memiliki satu buah titik sudut sebagai titik puncak
Rumus volume kerucut yaitu:
a. Volume Kerucut
- V = ⅓ x x r x r x t
Sementara itu cara menghitung luas permukaan kerucut yaitu dengan menghitung luas lingkaran yang dijumlahkan dengan luas lengkungan. Rumusnya menjadi seperti ini:
b. Luas Permukaan Kerucut
- L = ( x r x r) + ( x r x s)
Nilai s dapat dihitung menggunakan rumus phytagoras, sebagai berikut:
- s = r kuadrat + t kuadrat
Keterangan:
= Nilai phi adalah 22/7 untuk jari-jari kelipatan 7. Sedangkan untuk jari-jari selain kelipatan 7 menggunakan 3,14.
r = jari jari
t = tinggi
s = panjang rusuk atau garis pelukis. Dalam kerucut, garis pelukis yaitu garis yang menghubungkan titik puncak dengan titik keliling alas kerucut.
Baca Juga : Rumus Volume Kerucut: Contoh Soal dan Pembahasannya
3. Limas Segitiga
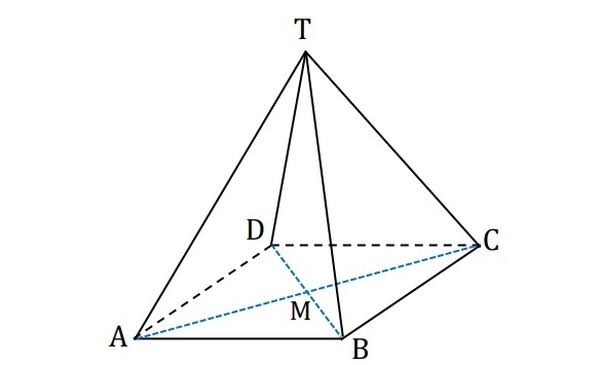
Bangun ruang berjenis limas memiliki sisi alas berbentuk sebuah segi banyak dan bangun segitiga yang mengerucut ke ke atas. Contoh limas dalam kehidupan sehari hari yaitu atap rumah, tenda, nasi bungkus, dan piramida Mesir.
Sementara itu, limas dikelompokkan menjadi beberapa jenis berdasarkan bentuk alasnya, seperti seperti limas segitiga, limas segi empat, limas segi lima, limas segi enam, dan lain sebagainya. Mari kita bahas satu per satu dimulai dari limas segitiga.
Limas segitiga memiliki beberapa sifat, seperti:
- Memiliki alas berbentuk segitiga
- Mempunyai bidang sisi tegak berbentuk segitiga
- Memiliki 4 buah titik sudut, 4 buah bidang sisi, dan 6 buah rusuk
- Tinggi limas segitiga terhitung dari jarak antara bidang alas dan titik puncak
Sementara itu, volume dan luas permukaan limas segitiga dapat dicari menggunakan rumus sebagai berikut:
a. Volume Limas Segitiga
- V = ⅓ x L alas x t
V = ⅓ x (½ as x ts) x t
b. Luas Permukaan Limas Segitiga
- L = L alas + L△I + L△II + L△III
Keterangan:
L alas = Luas alas
as = alas segitiga
ts = tinggi segitiga
t = tinggi
L△ = Luas selubung limas yang berbentuk segitiga
Baca Juga : Rumus Limas Segitiga Beserta Contoh Soal dan Pembahasan
4. Limas Segi Empat
Limas segi empat memiliki alas berbentuk segi empat yang bisa berupa persegi, persegi panjang, jajar genjang, atau segi empat lainnya. Sementara itu, sifat-sifat dari bangun ruang limas segi empat, yaitu:
- Memiliki 5 titik sudut dan 8 rusuk
- Terdiri dari 5 buah sisi yang terdiri dari 1 sisi alas dan 4 sisi tegak
- Sisi alas berbentuk segi empat
- Mempunyai 4 sisi tegak berbentuk segitiga
Berikut adalah rumus volume dan luas permukaan dari limas segi empat:
a. Volume Limas Segi Empat
- V = ⅓ x La x t
b. Luas Permukaan Limas Segi Empat
- Luas permukaan limas segi empat = luas alas + luas sisi
L = La + L△ I + L△ II + L△ III + L△ IV
Keterangan:
La = Luas alas
L△ = Luas segitiga
Baca Juga : Limas Segi Empat: Sifat, Rumus, Latihan Soal, dan Pembahasan
Latihan Soal dan Pembahasan
Setelah mengetahui rumus luas permukaan dan volume dari kubus, limas, dan kerucut, saatnya mengaplikasikan rumus tersebut dengan latihan soal di bawah ini. Cobalah untuk praktik mengerjakan soal agar kamu bisa belajar dan memahami rumus bangun ruang.
Contoh Soal Kubus
Sebuah kubus diketahui memiliki panjang rusuk 15 cm. Hitung berapa volume kubus tersebut!
Jawaban: 375 cm3
Pembahasan:
Diketahui r = 15 cm
Ditanya= volume?
V = r x r x r = 15 x 15 x 15 = 375
Maka, volume kubus tersebut adalah 375 cm3
Contoh Soal Kerucut
Diketahui sebuah kerucut memiliki jari-jari 7 cm, tinggi 9 cm, dan garis pelukis 12 cm. Berapakah volume dan luas permukaannya?
Jawaban: Volume = 462 cm3, Luas permukaan = 418 cm2.
Pembahasan:
V = ⅓ x x r x r x t
V = ⅓ x 22/7 x 7 x 7 x 9
V = 462 cm3
Untuk mencari luas permukaan, menggunakan rumus:
L = ( x r x s) + ( x r x r)
L = (22/7 x 7 x 12) + (22/7 x 7 x 7)
L = 264 + 154
L = 418 cm2
Maka, luas permukaan dari kerucut tersebut yaitu 418 cm2, sedangkan volumenya adalah 462 cm3.
Contoh Soal Limas Segitiga
Jika diketahui suatu limas segitiga memiliki tinggi 7 cm, tinggi segitiga alas 6 cm, dan alas segitiga 13 cm. Berapa volume dari limas tersebut?
Jawaban: V = 91 cm3
Pembahasan:
V = ⅓ x La x t
V = ⅓ x (½ x as x ts) x t
V = ⅓ x (½ x 13 x 6) x 7
V = ⅓ x 39 x 7
V = 91 cm3
Maka, volume dari limas segitiga tersebut adalah 91 cm3.
Contoh Soal Limas Segi Empat
Sebuah limas persegi empat memiliki panjang alas 6 cm dan tinggi sisi tegak segitiganya 4 cm. Berapakah luas dan volumenya?
Jawaban: Luas permukaan = 96 cm2 dan Volume = 48 cm3.
Pembahasan:
Mencari luas permukaan limas segi empat menggunakan rumus L = La + L△ I + L△ II + L△ III + L△ IV
Karena alasnya adalah persegi empat, maka luas alasnya (La) adalah:
La = s x s
La = 6 cm x 6 cm
La = 36 cm2
Sedangkan untuk L△ dapat dihitung menggunakan rumus phytagoras:
c2 = a2 + b2
c2 = 42 + 32
c2 = 16 + 9
c2 = 25
c2 = 5 cm
Maka L△ dapat dihitung dengan:
L△I = ½ x a △ 1 x t △ 1
L△I = ½ x 6 x 5 = 15 cm2
Sehingga, luas permukaan limas segi empat menjadi:
L = La + L△ I + L△ II + L△ III + L△ IV
L = 36 cm2 + 15 cm2 + 15 cm2 + 15 cm2 + 15 cm2
L = 96 cm2
Maka, luas permukaan limas segi empat adalah 96 cm2.
Sedangkan untuk mencari volume limas segi empat menggunakan rumus:
V = ⅓ x L alas x t
V = ⅓ x (s x s) x t
V = ⅓ x (6 x 6) x 4
V = 48 cm3
Jadi, volume limas segi empat adalah 48 cm3.
Baca Juga : Mengenal Bangun Ruang: Macam, Sifat, Rumus, dan Pembahasan Soal
Sudah Paham Rumus Bangun Ruang?
Itulah rumus bangun ruang pada bangun kubus, kerucut, dan limas. Masing-masing bangun ruang memiliki rumus berbeda untuk menghitung volume dan luas permukaannya. Cobalah untuk sering mengerjakan latihan soal untuk mengasah pemahamanmu tentang bangun ruang. Semoga berhasil!

