Kerucut merupakan salah satu bentuk geometri tiga dimensi atau bangun ruang yang mempunyai bentuk lingkaran di bagian alasnya. Sementara secara dua dimensi akan tampak seperti bentuk segitiga sama sisi. Sebagai bangun ruang, tentu ada rumus untuk menghitung luas permukaan dan rumus volume kerucut.
Gambaran paling sederhana tentang bangun ruang kerucut adalah topi ulang tahun. Kamu bisa membayangkan adanya bagian lingkaran dan selimut di sisi serta puncaknya? Nah, untuk mengetahui lebih jelas, artikel kali ini akan mengulas tentang unsur-unsur kerucut, rumus volume, hingga contoh soal dan jawabannya.
Rumus Volume Kerucut
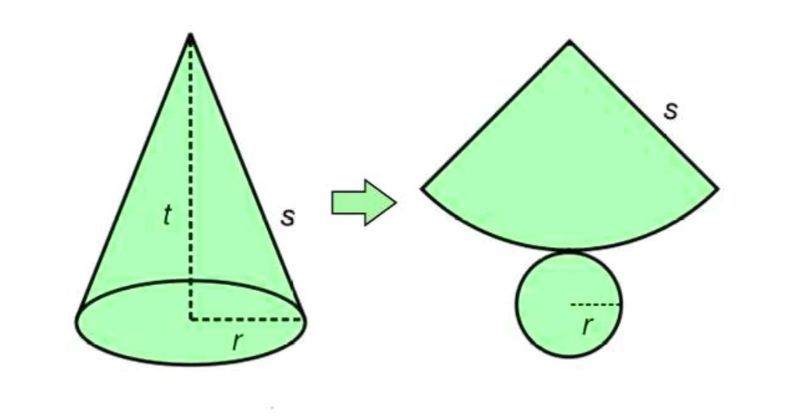
Rumus volume kerucut, antara lain:
Volume = 1/3 x luas alas x tinggi
Dalam hal ini, alas bangun kerucut adalah lingkaran. Maka, rumus detail untuk menghitung volumenya adalah:
Volume (V) = π x r x r x t
Sementara satuan volume kerucut adalah kubik atau lambang pangkat tiga. Misalnya, meter kubik (cm3).
Keterangan:
- V = volume
- r = jari-jari
- t = tinggi
- π(phi) = 22/7 atau 3,14
Baca Juga : Rumus Limas Segitiga Beserta Contoh Soal dan Pembahasan
Rumus Volume Kerucut Terpancung
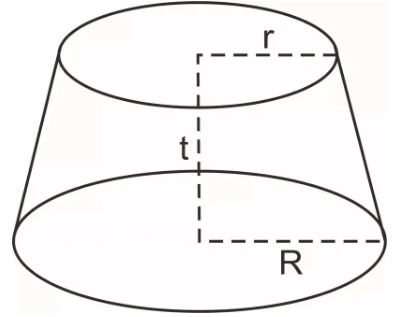
Tahukah kamu jika ada bangun kerucut yang tidak memiliki titik puncak? Kerucut jenis ini memiliki bagian puncak berbentuk lingkaran dan disebut sebagai kerucut terpancung. Berikut ini rumus untuk menghitung volume kerucut terpancung:
V = 1/3 × π x t x (r x R + r² + R²)
Unsur-Unsur Kerucut
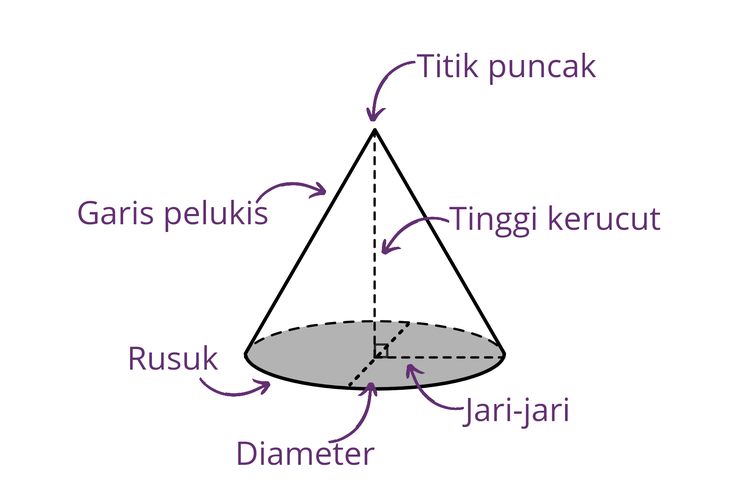
Berdasarkan rumus volume bangun kerucut di atas, ada beberapa unsur kerucut yang perlu kamu pahami. Berikut masing-masing unsurnya:
1. Jari-Jari Kerucut
Jari-jari pada kerucut merupakan istilah yang mewakili radius alas kerucut. Kamu bisa mengetahui jari-jari dengan menghitung jarak antara lingkaran alas terhadap titik pusat lingkaran tersebut.
Istilah lain menyebutkan bahwa jari-jari adalah setengah dari diameter lingkaran alas. Sedangkan diameter alas pada kerucut adalah jarak garis lurus antara permukaan lingkaran alas dan permukaan di sebelahnya, dengan melalui titik pusat lingkaran.
2. Tinggi Kerucut
Unsur lain yang terdapat pada rumus volume bangun adalah tinggi. Tinggi kerucut merupakan jarak antara titik pusat lingkaran alas dan titik puncak kerucut.
3. Garis Pelukis
Unsur selanjutnya, yaitu garis pelukis. Garis pelukis atau selimut kerucut merupakan sisi lengkung yang membungkus kerucut. Sisi lengkung kerucut ini berada di bagian sisi kanan dan kiri kerucut.
4. Bidang Alas
Bidang alas adalah ruas garis yang menghubungkan dua titik pada lingkaran melalui titik pusat lingkaran alas. Biasanya, bidang alas pada kerucut juga dilambangkan dengan “phi”.
Contoh Soal Volume Kerucut
Agar Anda lebih paham dengan rumus volume kerucut, simak berbagai contoh soal di bawah ini!
Contoh 1
Sebuah bangun ruang kerucut memiliki jari-jari sisi alas 7 cm dan tinggi 6 cm. Berapakah volume bangun tersebut?
Penyelesaian:
Volume = 1/3 x π x r x r x t
= 1/3 x 22/7 x 7 x 7 x 6
= 1/3 x 22/7 x 49 x 6
= 1/3 x 924 = 308 cm³
Jadi, bangun kerucut tersebut memiliki volume senilai 308 cm³.
Contoh 2
Sebuah kerucut mempunyai diameter sisi alas 28 cm dan tinggi 12 cm. Maka, hitunglah volumenya menggunakan rumus volume kerucut!
Penyelesaian:
Jari-jari = 1/2 x diameter= 1/2 x 28 = 14 cm
Maka,
Volume = 1/3 x π x r x r x t
= 1/3 x 22/7 x 14 x 14 x 12
= 1/3 x 22/7 x 196 x 12
= 1/3 x 7.392 = 2.464 cm³
Contoh 3
Tentukan volume dari kerucut yang memiliki jari-jari 10,5 cm dan tinggi 20 cm!
Penyelesaian:
Volume = 1/3 x π x r x r x t
= 1/3 x 3,14 x 10,5 x 10,5 x 20
= 115,4 x 20 = 2,308 cm3
Jadi, bangun kerucut tersebut memiliki volume senilai 2,308 cm³.
Contoh 4
Terdapat sebuah kerucut dengan sisi alas berdiameter 20 cm. Apabila tinggi kerucut 12 cm, berapakah volume bangun tersebut, jika kamu hitung dengan rumus volume kerucut?
Penyelesaian:
Jari-jari = 1/2 x diameter= 1/2 x 20 = 10
Maka,
Volume = 1/3 x π x r x r x t
= 1/3 x 3,14 x 10 x 10 x 12
= 1/3 x 3,14 x 100 x 12 = 1.256 cm³
Jadi, bangun kerucut tersebut memiliki volume senilai 1.256 cm³.
Contoh 5
Diketahui sebuah bangun kerucut terpancung mempunyai jari-jari atas 5 cm, jari-jari bawah 6 cm, dan tinggi 10 cm. Selanjutnya, tentukan volume bangun tersebut!
Penyelesaian:
Volume = 1/3xπxt(R2 + Rxr + r2)
= 1/3 x 3,14 x 12(102 + 10×5 + 52)
= 1/3 x 3,14 x 12(100 + 50 + 25)
= 1/3 x 3,14 x 12(175)
= 1/3 x 3,14 x 2.100
= 1/3 x 6.594 = 2.198 cm³
Jadi, kerucut terpanjung ini mempunyai volume senilai 2.198 cm³.
Contoh 6
Sebuah kerucut terisi penuh oleh air sebanyak 5.024 cm3 dengan jari-jari alas 10 cm. Maka, berapakah tinggi air pada kerucut tersebut, bila kamu hitung dengan rumus volume kerucut?
Penyelesaian:
Volume = 1/3 x π x r x r x t
5.024 = 1/3 x 3,14 x 10 x 10 x t
5.024 x 3 = 314 x t
48 = t
Jadi, tinggi air pada kerucut di atas adalah 48 cm.
Contoh 7
Terdapat tumpukan garam yang berbentuk kerucut dengan tinggi 12 m dan diameter alas 30 m. Jika volume tumpukan garam yang bisa diangkut sebuah truk adalah 80 m3, maka berapa jumlah truk yang dibutuhkan untuk mengangkut semua tumpukan garam?
Penyelesaian:
Jari-jari = 1/2 x diameter= 1/2 x 30 = 15
Maka,
Volume = 1/3 x π x r x r x t= 1/3 x 3,14 x 15 x 15 x 12 = 2.826 m3.
Sebelumnya, volume angkut satu truk adalah 80 m3. Maka, 2.826 / 80 = 35,3. Jadi, truk yang dibutuhkan untuk mengangkut tumpukan garam adalah 36 truk, bila kita bulatkan.
Contoh 8
Bangun kerucut terdiri dari jari-jari 14 cm dan tinggi 54 cm. Tentukan volume dari bangun tersebut memakai rumus volume kerucut?
Penyelesaian:
Volume = 1/3 × π × r × r × t
= 1/3 × 22/7 × 14 × 14 × 54
= (1/3 × 54) × (22/7 × 14) × 14
= 18 × 44 × 14 = 11.088 cm3
Jadi, bangun kerucut tersebut memiliki volume senilai 11.088 cm³.
Contoh 9
Diketahui volume sebuah kerucut adalah 462 cm2. Apabila tingginya 9 cm, berapakah jari-jari kerucut tersebut?
Penyelesaian:
Volume = 1/3 × π × r2 × t
462 = 1/3 x 22/7 x r2 x 9
r2 = 462 x 7/22 x 3 / 9
= 21 x 7 x 3 / 9
= 441 / 9 = 49
r = √49 = 7
Jadi, panjang jari-jari pada bangun kerucut di atas adalah 7 cm.
Contoh 10
Sebuah kerucut mempunyai tinggi 20 cm dan volume 8.300 cm3. Berapakah panjang jari-jarinya?
Penyelesaian:
Volume =1/3× π × r² × t
8.300 = 1/3 × 3,14 × r² × 20
8.300 =21 × r²
r² = 8.300/21
r² = 395,2
r = √395,2 =19,8
Jadi, panjang jari-jari kerucut adalah 19,8 atau bisa dibulatkan menjadi 20 cm.
Baca Juga : Rumus Bola (Luas, Keliling, Volume), Contoh, dan Pembahasan
Sudah Paham Rumus Volume Kerucut dan Cara Menghitungnya?
Bangun ruang kerucut terdiri dari beberapa unsur, seperti jari-jari, tinggi kerucut, garis pelukis atau selimut, dan bidang alas. Unsur-unsur tersebut terdapat dalam rumus untuk menghitung volume kerucut.
Selain itu, ada beberapa contoh soal untuk menambah pemahaman kamu dalam belajar menghitung volume bangun ruang ini yang bisa kamu dapatkan di internet maupun di buku sekolah.

