Fungsi trigonometri dalam ilmu matematika, yakni mempelajari tentang fungsi dari sebuah sudut, untuk menghubungkan antara sudut-sudut dan sisi-sisi yang ada di sebuah segitiga. Berbicara tentang trigonometri, tentu membuat kamu ingat dengan istilah sudut istimewa maupun rumus sin cos tan.
Ada cara yang mudah untuk mengingat dan memahami terkait sudut-sudut dalam trigonometri melalui tabel sudut istimewanya. Kamu juga bisa mengingat apakah nilai sin, cos, dan tan berupa positif atau negatif di setiap kuadran. Untuk memperdalam pemahaman kamu, simak terus ulasan di bawah ini!
Pengertian Rumus Sin Cos Tan dalam Trigonometri
Trigonometri merupakan suatu ilmu yang mempelajari seputar sudut dan fungsinya. Kamu bisa mempelajari trigonometri untuk mengetahui hubungan antara sudut-sudut dan sisi-sisi segitiga yang disebut fungsi trigonometri. Sementara fungsi dasar dari trigonometri, antara lain sin, cos, tan, cot, sec, dan cosec.
Dalam hal ini, segitiga dalam fungsi trigonometri berupa segitiga siku-siku, dimana terdapat satu sudut yang bernilai 90 derajat. Sisi segitiga siku-siku yang terdiri dari sisi tegak lurus, sisi miring, dan sisi alas nantinya digunakan untuk menentukan nilai sin, cos, dan tan.
Rumus Sin Cos Tan
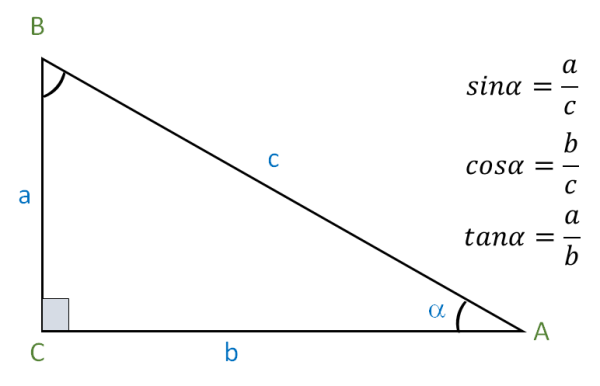
Berikut penjelasan dari rumus dasar sinus, cosinus, dan tangen yang perlu kamu pahami:
1. Sinus (Sin)
Sin atau sinus merupakan perbandingan panjang segitiga antara sisi yang berada di depan sudut, dengan sisi miring pada segitiga siku-siku. Jadi, rumusnya berupa depan/miring (Sin α = b/c).
2. Cosinus (Cos)
Cos atau cosinus merupakan perbandingan panjang segitiga, antara sisi samping sudut dan sisi miring pada segitiga siku-siku. Sehingga, rumusnya adalah samping/miring (Cos α = a/c).
3. Tangen (Tan)
Tan atau tangen adalah perbandingan panjang sisi segitiga yang berada di depan sudut dan sisi samping pada segitiga siku-siku. Rumusnya yaitu depan/samping (Tan α = b/a).
Baca Juga : Turunan Fungsi Trigonometri: Pengertian, Rumus, dan Contoh Soal
Sudut Istimewa Rumus Sin Cos Tan
Kamu tentu sudah tahu jika segitiga memiliki tiga sisi yang berada di depan, samping, dan miring. Jumlah total sudut yang terbentuk dalam bangun segitiga adalah 180 derajat. Nah, di antara berbagai sudut dalam segitiga, terdapat beberapa sudut istimewa. Sudut istimewa ini biasanya digunakan dalam fungsi trigonometri.
Sudut istimewa merupakan sudut yang mempunyai nilai perbandingan trigonometri dan dapat diketahui dengan cara mudah dan cepat. Bahkan, tanpa menggunakan kalkulator. Sudut istimewa tersebut antara lain 0, 30, 45, 60, dan 90 derajat. Setiap sudut istimewa ini mempunyai rumus sin, cos, tan yang berbeda di setiap kuadran.
Selain itu, apabila terdapat sudut selain sudut istimewa dan ingin kamu ubah menjadi sudut istimewa, maka gunakan nilai sudut 90, 180, 270, dan 360 derajat sebagai patokan. Ini agar sudut tersebut mengandung sudut istimewa di kuadran I.
Apabila kamu menggunakan dasar nilai sudut 90 dan 270, maka konsepnya berubah, yaitu sin menjadi cos, tan menjadi cotan, dan cos menjadi sin. Jika kamu menggunakan nilai sudut 180 dan 360 derajat, maka tidak ada perubahan nilai.
Baca Juga : Sudut Istimewa Trigonometri: Contoh Soal & Pembahasannya
Tabel Rumus Sin Cos Tan
Berikut ini beberapa ketentuan penghitungan sin, cos, dan tan berdasarkan masing-masing kuadran:
1. Tabel Kuadran I
| Sudut | sin | cos | tan |
| 0o | 0 | 1 | 0 |
| 30o | 1/2 | 1/2√ 3 | 1/3√ 3 |
| 45o | 1/2√ 2 | 1/2√ 2 | 1 |
| 60o | 1/2√ 3 | 1/2 | √ 3 |
| 90o | 1 | 0 | ~ |
2. Tabel Kuadran II
| Sudut | sin | cos | tan |
| 90o | 1 | 0 | Tak terdefinisi |
| 120o | 1/2√3 | -1/2 | -√3 |
| 135o | 1/2√2 | -1/2√2 | -1 |
| 150o | 1/2 | -1/2√3 | -1/3√3 |
| 180o | 0 | -1 | 0 |
3. Tabel Kuadran III
| Sudut | sin | cos | tan |
| 180o | 0 | -1 | 0 |
| 210o | -1/2 | -1/2√3 | 1/3√3 |
| 225o | -1/2√2 | -1/2√2 | 1 |
| 240o | -1/2√3 | -1/2 | √3 |
| 270o | -1 | 0 | Tak terdefinisi |
4. Tabel Kuadran IV
| Sudut | sin | cos | tan |
| 270o | -1 | 0 | Tak terdefinisi |
| 300o | -1/2√3 | 1/2 | -√3 |
| 315o | -1/2√2 | 1/2 | -1 |
| 330o | -1/2 | 1/2√2 | -1/3√3 |
| 360o | 0 | 1 | 0 |
Ketentuan Kuadran pada Rumus Sin Cos Tan
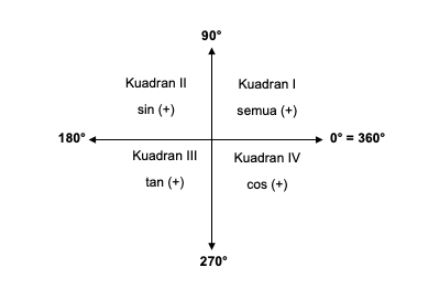
Tidak hanya sudut istimewa, ada pula konsep kuadran untuk menentukan nilai sin, cos, dan tan bernilai positif atau negatif. Berikut ini ketentuannya:
1. Kuadran I
Area pada kuadran I terdiri dari sudut istimewa 0, 30, 45, 60, dan 90 derajat. Pada kuadran ini, menunjukkan nilai dari sin, cos, dan tan positif. Agar lebih mudah mengingatnya, kamu bisa menggunakan kata kunci “Semua”.
2. Kuadran II
Area pada kuadran II terdiri dari sudut istimewa 90, 120, 135, 150, dan 180 derajat. Pada kuadran II menunjukkan nilai sin positif. Sedangkan nilai cos dan tan negatif. Jadi, kamu bisa mengingatnya dengan kata kunci “Sindikat”.
3. Kuadran III
Area pada kuadran III terdiri dari sudut 180, 210, 225, 240, dan 270 derajat. Pada kuadran III menunjukkan hanya nilai tan yang positif. Kamu bisa mengingatnya dengan kata kunci “Tangan”.
3. Kuadran IV
Area pada kuadran IV terdiri dari sudut 270, 300, 315, 330, dan 360 derajat. Pada kuadran IV menunjukkan hanya nilai cos yang positif. Sedangkan nilai sin dan tan negatif.
Contoh Soal dan Pembahasan
Berikut beberapa contoh soal dan pembahasannya untuk membantu kamu dalam menerapkan rumus sin cos tan untuk berbagai situasi:
Contoh 1
Diketahui sebuah segitiga siku-siku, dimana salah satu sudutnya 60 derajat dan panjang sisi miring 12 cm. Berapakah panjang sisi depan sudut (d)?
Pembahasan:
Cara mendapatkan nilai panjang sisi depan sudut pada segitiga bisa menggunakan persamaan sin seperti berikut.
Sin 60 derajat = d/12
1/2 √3 = d/12
12/2 √3 = d
d = 6√3 cm
Jadi, panjang sisi depan sudut (d) pada segitiga tersebut adalah 6√3 cm.
Contoh 2
Tentukan nilai trigonometri dari tan 315.
Pembahasan:
Pertama, kamu perlu mengetahui jika sudut 315 derajat berada di kuadran IV, sehingga nilainya negatif. Berikut ini cara menghitungnya:
tan(315o) = tan(360o – 45o)
tan(360o – 45o)= – tan(45o)
tan(315o) = -1
Jadi, nilai dari tan 315 adalah -1.
Contoh 3
Tentukan nilai dari cos 210!
Pembahasan:
Pertama, kamu harus mengetahui bahwa sudut 210 berada di kuadran III. Aturan kuadran III adalah hanya tan yang bernilai positif, itu artinya nilai cos adalah negatif.
Kedua, karena tidak termasuk sudut istimewa, maka kamu perlu menghitung sudut terdekat dari sudut 210 pada tabel sudut istimewa. Nilai sudut terdekatnya adalah 180 derajat. Berikut perhitungan selanjutnya:
Cos 210 = cos (180 + 30)
Cos 210 = -cos 30 = -½√3
Jadi, nilai cos 210 adalah -½√3.
Contoh 4
Tentukan nilai trigonometri dari sin 210.
Pembahasan:
Sudut 210 terletak di kuadran III sehingga sin bernilai negatif. Berikut ini cara selanjutnya:
Sin (210o) = sin (180o + 30o)
Sin (180o + 30o) = -sin(30o)
= -1/2
Jadi, nilai dari sin 210 adalah -1/2.
Sudah Lebih Paham Seputar Rumus Sin Cos Tan?
Pada dasarnya, sinus, cosinus, dan tangen adalah bagian utama dari trigonometri. Ada beberapa sudut istimewa yang bisa menjadi acuan dalam menentukan nilai sudutnya, seperti 0, 30, 45, 60, dan 90 derajat. Kamu juga bisa mengetahui sin, cos, tan bernilai positif atau negatif melalui aturan di kuadran I, II, III, dan IV.

