Kamu tahu tidak apa itu trigonometri? Pelajaran matematika ini berhadapan dengan sudut segitiga. Pasti kamu juga pernah mendengar sinus, cosinus dan tangen bukan pada rumus segitiga? Nah, kali ini kita akan mempelajari sudut istimewa trigonometri.
Pengertian Sudut
Sudut adalah daerah yang terbuat dari dua garis yang berpotongan. Misalnya, dua jarum jam yang menunjukkan pukul 3.
Nah, itu akan membentuk sudut, apabila kamu ukur menggunakan busur. Untuk mempelajari sudut, berikut ini rumus mengenai sudut yang dapat kamu pelajari, yaitu:
- Ukuran Sudut Dalam Derajat
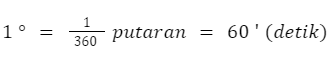
- Ukuran Sudut Dalam Radian
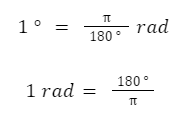
Berdasarkan rumus diatas dapat kamu simpulkan, mengukur sudut itu penting sekali.
Ukuran sudut antara derajat dan radian sangat berbeda dan memiliki besaran sudut yang berbeda juga. Apalagi untuk sudut trigonometri yang akan kamu pahami berikut ini.
Pengertian Trigonometri
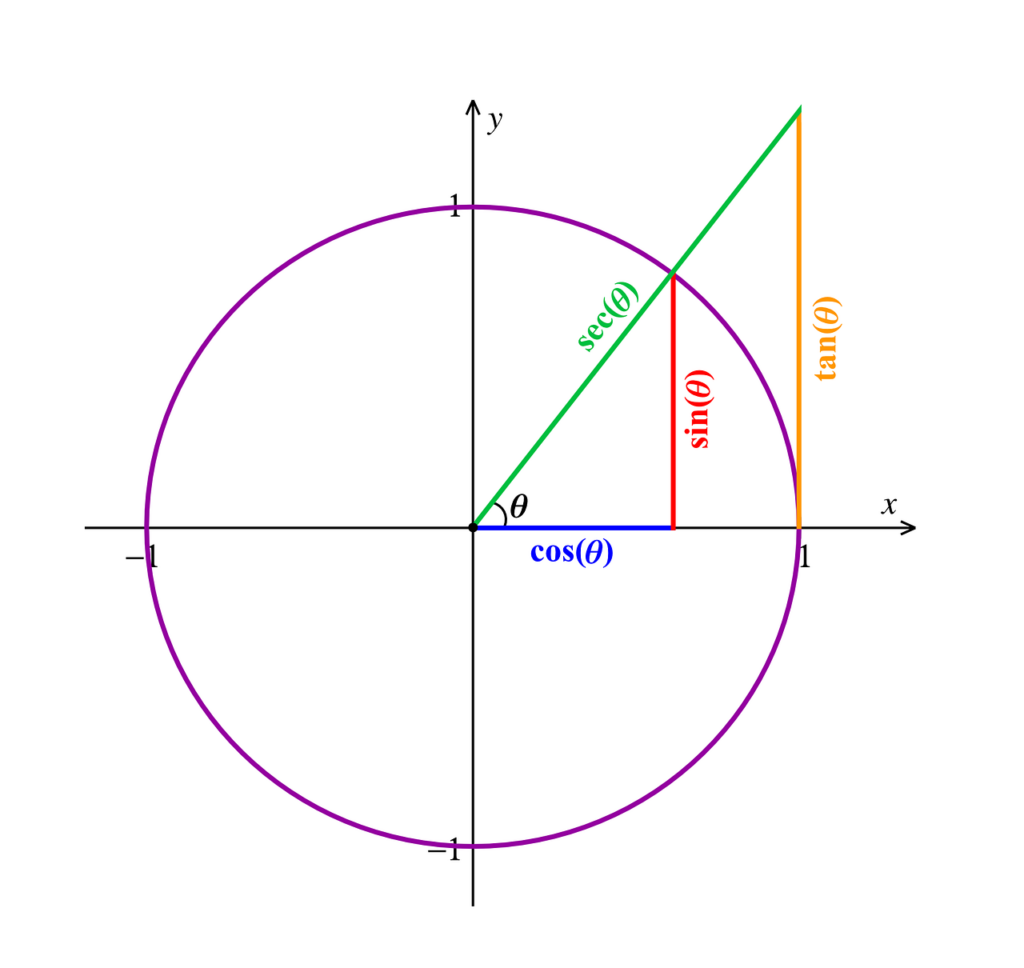
Trigonometri berasal dari dua buah kata yaitu “trigonon” dan “metron”. Trigonon adalah tiga sudut. Tiga sudut tersebut bisa kamu lihat pada bangun segitiga. Sedangkan metron adalah mengukur.
Jadi trigonometri adalah ilmu yang membahas ukuran sudut, garis, dan sisi yang ada pada segitiga. Ilmu trigonometri biasanya untuk navigasi di laut, udara, dan angkasa, teori musik, astronomi, dan menghitung luas segitiga.
Dalam sebuah bangun segitiga, terdapat sudut sudut istimewa. Khususnya segitiga siku-siku. Terdapat sinus, cosinus, tangen, cos, cotangen, dan lainnya seperti yang ada pada gambar.
Aturan tentang sinus berguna untuk menghubungkan sisi segitiga dengan sudutnya. Sedangkan, aturan cosinus berfungsi untuk menghubungkan ketiga sisi segitiga ke satu sudut.
Untuk menghitung sudut pada segitiga yang ada pada lingkaran, kamu harus tahu segitiga tersebut masuk di bagian kuadran mana.
Pada lingkaran dibagi menjadi empat bagian yaitu Kuadran I, II, III dan IV. Penjelasan mengenai kuadran yakni sebagai berikut, yaitu:
| Kuadran | Rentang Sudut | Nilai |
| I | 0° – 90° | Sinus (+), Cosinus (+), dan Tangen (+) |
| II | 90° – 180° | Sinus (+) , Cosinus(-), dan Tangen (-) |
| III | 180° – 270° | Sinus (-) , Cosinus(-), dan Tangen (+) |
| IV | 270° – 360° | Sinus (-) , Cosinus(-), dan Tangen (-) |
Sudut Istimewa Trigonometri
Sudut istimewa trigonometri adalah sudut tertentu yang memiliki nilai tanpa perlu kamu hitung manual menggunakan kalkulator. Sudut ini yakni sudut 0°, 30°, 45°, 60°, dan 90°.
Sudut ini dalam matematika dihitung berdasarkan sin, cos, tan, cosecan, secan, cotangen. Simak penjelasannya pada tabel ini.
| 0° | 30° | 45° | 60° | 90° | 120° | 180° | 270° | 360° | |
| Sin | 0 | 1/2 | √2/2 | √3/2 | 1 | √3/2 | 0 | -1 | 0 |
| Cos | 1 | √3/2 | √2/2 | 1/2 | 0 | -1/2 | -1 | 0 | 1 |
| Tan | 0 | 1/√3 | 1 | √3 | Tak hingga | -√3 | 0 | Tak hingga | 0 |
| Cotan | Tak hingga | √3 | 1 | 1/√3 | 0 | -1/√3 | Tak hingga | 0 | Tak hingga |
| Secan | 1 | 2/√3 | √2 | 2 | Tak hingga | -2 | -1 | Tak hingga | 1 |
| Cosec | Tak hingga | 2 | √2 | 2/√3 | 1 | 2/√3 | Tak hingga | -1 | Tak hingga |
Tabel diatas merupakan tabel penetapan dari sudut sudut segitiga. Jadi jika kita tarik kesimpulan, maka sebagai berikut.
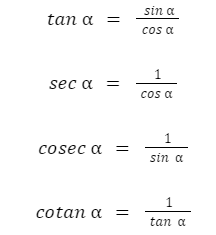
Identitas Trigonometri
Identitas trigonometri adalah hubungan antara fungsi dalam trigonometri yang menghasilkan kesamaan perbandingan sudut. Hubungan tersebut berisi pernyataan, ruas kiri dan ruas kanan memiliki kesamaan fungsi dalam trigonometri. Berikut 3 identitas trigonometri, yaitu:
a. Konsep Identitas Kebalikan
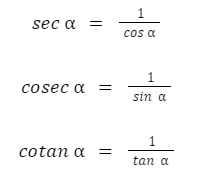
b. Konsep Komparasi
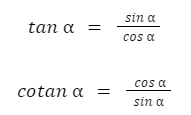
c. Konsep Phytagoras
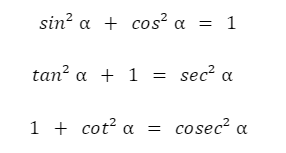
Perbandingan Trigonometri
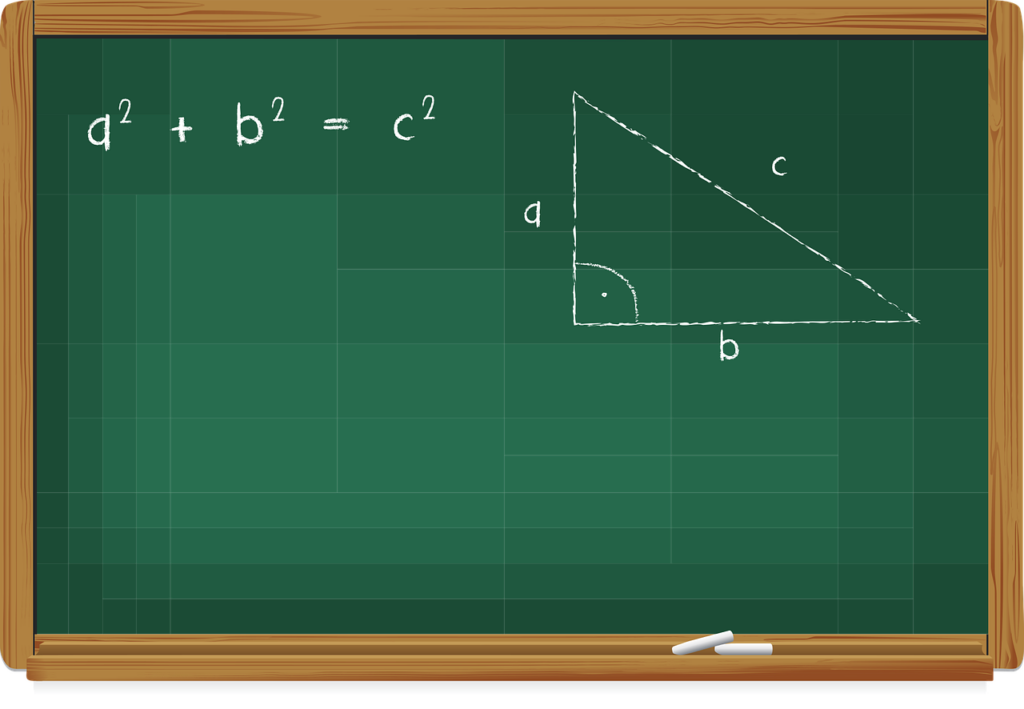
Seperti yang telah dijelaskan di atas, pada trigonometri kita akan membahas tentang sudut, identitas, dan perbandingan dalam sebuah segitiga. Supaya kamu lebih paham, mari perhatikan penjelasan segitiga di bawah ini.
Pada segitiga di atas, terdapat 3 buah sisi yang mengacu pada sudut . Nah ketiga sisi tersebut yakni sebagai berikut :
- a = sisi depan yang menghubungkan titik A dan B
- b = sisi samping yang menghubungkan titik B dan C
- c = sisi miring yang menghubungkan titik A dan C
Dalam mencari perbandingan trigonometri pada segitiga siku-siku di atas, terdapat rumus yang harus kamu hafal. Untuk memudahkan hafalanmu ada singkatan persamaan.

Selain itu dari rumus diatas kamu akan memperoleh sudut yang lainnya yaitu :

5 Contoh Soal Sudut Istimewa Trigonometri

Berikut 5 contoh soal tentang materi sudut istimewa trigonometri yang dapat kamu pelajari, yaitu:
Contoh Soal 1
Tentukan nilai dari sin 90° + cos 60° =
Jawab =
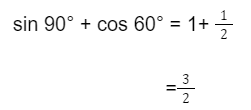
Contoh Soal 2
Ubah sudut berikut menjadi radian
- 100°
- 210°
Jawab =
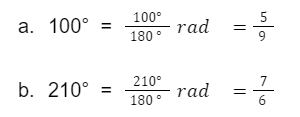
Contoh Soal 3
Berapa nilai sin 150°?
Jawab =
Sin 150° = Sin (180° -150°)
= Sin 30°
Karena nilai sinus di kuadran II bernilai positif, maka nilai sinus 150°=sinus 30° = ½.
Contoh Soal 4
Sebuah menara tinggi berdiri tegak lurus di pinggir danau. Dengan jarak 100 meter dari ujung menara ke permukaan danau, seorang pengamat melihat ujung menara dari sudut 30 derajat terhadap permukaan air. Bagaimana menghitung tinggi menara tersebut?
Jawab:
Dalam situasi ini, sudut 30 derajat antara pengamat dan permukaan air dapat dianggap sebagai sudut trigonometri khusus. Kita sebut tinggi menara tersebut sebagai h.
Tinggi menara / Jarak menara ke permukaan air = Tangen 30°
h / 100 = (√3)/3
h = 100 × (√3)/3
h = 57.74 meter
Jadi, tinggi menara tersebut adalah sekitar 57.74 meter.
Contoh Soal 5
Tentukan nilai dari: 2 cos 75° cos 15°
Jawab:
2 cos 75° cos 15° = cos [75 +15]° + cos [75 – 15]°
= cos 90° + cos 60°
= 0 + ½
= ½
Baca Juga : Turunan Fungsi Trigonometri: Pengertian, Rumus, dan Contoh Soal
Sudah Paham Sudut Istimewa Trigonometri?
Itulah penjelasan mengenai sudut istimewa trigonometri beserta identitas trigonometri, perbandingan trigonometri, dan contoh soalnya. Dengan membaca artikel ini, kamu tidak perlu bingung lagi menghadapi berbagai soal terkait sudut istimewa ini.
Namun, agar lebih mahir pastikan kamu belajar dan latihan mengerjakan soal setiap hari. Dengan begitu, kamu akan semakin pandai dalam materi ini.

