Sistem persamaan linear tiga variabel (SPLTV) yang merupakan bagian dari ilmu Matematika di jenjang SMA memang merupakan salah satu materi yang cukup sulit. Tapi, kalau kamu bisa menguasainya dengan baik, ilmu ini bisa kamu manfaatkan dalam banyak aspek kehidupan, lo!
Simak penjelasan materi persamaan linear yang spesifik ini lewat pembahasan berikut!
Apa Itu Sistem Persamaan Linear Tiga Variabel (SPLTV)?
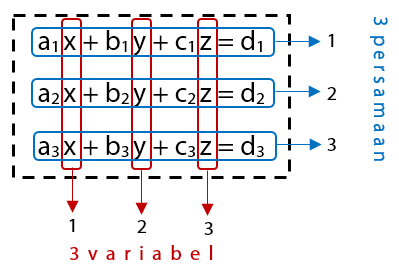
Sistem persamaan linear tiga variabel adalah salah satu konsep Matematika yang menjelaskan relasi atau persamaan linear yang masing-masing memiliki tiga variabel, misalnya (x), (y), dan (z).
Apa contoh penerapan dari konsep sistem persamaan linier tiga variabel?
Kamu bisa mengambil contoh ketika membeli beberapa kebutuhan pokok di warung, seperti kopi, garam, dan gula.
Ketika membeli ketiga barang tersebut, kamu tidak memperhatikan harga masing-masing barang Tetapi, kamu hanya mengambil sesuai kebutuhan (misalnya dalam satuan gram atau kilogram) dan membayar harga yang disebutkan penjaga warung.
Ketika sampai rumah, kamu ingin mengetahui berapa harga kopi, garam, dan gula per satuannya. Nah, kamu bisa mencari tahu harga barang-barang tersebut kalau memahami konsep sistem persamaan linear tiga variabel (SPLTV).
Sebenarnya, SPLTV memiliki konsep yang mirip dengan sistem persamaan linier dua variabel (SPLDV). Hanya saja, di SPLTV l, jumlah variabel yang terlibat lebih banyak.
Agar lebih jelas, kamu bisa melihat bentuk umum SPLTV) di bawah ini.

Jika kamu tulis bentuk tersebut ke dalam soal, maka bentuknya adalah sebagai berikut:
x + y – z = 4
3x – y + 2z = 9
x + 2y – z = 6
Nah, bagaimana cara kamu untuk mencari tahu nilai (x), (y), dan (z), jika diketahui tiga persamaan di atas? Yuk, kamu simak pembahasan bagian dari materi berikutnya agar kamu makin paham tentang materi ini!
Baca Juga : Persamaan Linear Dua Variabel: Metode Grafik dan Substitusi
Ciri-ciri Sistem Persamaan Linear Tiga Variabel
Agar kamu mudah untuk menyelesaikan permasalahan yang berhubungan dengan persamaan linear spesifik ini, kamu harus tahu dahulu apa saja ciri-ciri dari SPLTV dalam rincian di bawah ini.
- Sistem persamaan linier tiga variabel menggunakan tanda sama dengan (=) untuk relasinya.
- Memiliki tiga variabel, biasanya dilambangkan dengan huruf (x), (y), dan (z).
- Ketiga variabel tersebut berpangkat satu.
Menyelesaikan Sistem Persamaan Linear Tiga Variabel, Bagaimana Caranya?
Ada dua cara untuk menyelesaikan permasalahan yang membutuhkan konsep sistem SPLTV, yaitu dengan cara eliminasi dan substitusi. Bagaimana langkah menggunakan kedua cara tersebut? Lalu, kira-kira cara mana yang lebih mudah? Langsung saja kamu cari tahu!
1. Metode Eliminasi
Metode eliminasi adalah cara pertama yang bisa kamu pakai untuk menyelesaikan soal sistem persamaan linear tiga variabel (SPLTV).
Konsep dari metode eliminasi ini adalah kamu bisa menghilangkan salah satu dari tiga variabel yang tersedia, baik itu variabel (x), (y), dan (z). Kamu bisa memilih dengan bebas.
Agar kamu dapat bayangan cara pengaplikasian metode ini, langsung saja gunakan contoh soal yang sudah kamu sempat lihat di atas.
x + y – z = 4 (persamaan 1)
3x – y + 2z = 9 (persamaan 2)
x + 2y – z = 6 (persamaan 3)
Agar kamu bisa mengetahui nilai (x), (y), dan (z), kamu bisa mengeliminasi salah satu variabel agar lebih mudah menemukan variabel lainnya. Misal, kamu ingin menghapus variabel (y). Ambil 2 persamaan.
x + y – z = 4 (persamaan 1)
3x – y + 2z = 9 (persamaan 2)
Kamu bisa eliminasi variabel (y) dengan cara menambahkan kedua persamaan tersebut. Mengapa? Alasannya karena y + (-y) akan habis.
Jadi, kamu akan mendapatkan persamaan linier dua variabel baru, yaitu:
4x + z = 13
Kemudian, kamu ambil kembali 2 persamaan tiga variabel yang lain. Misalnya persamaan 2 dan 3.
3x – y + 2z = 9 (persamaan 2)
x + 2y – z = 6 (persamaan 3)
Sama dengan mencari sistem persamaan linier dua variabel sebelumnya, kamu bisa mengeliminasi variabel manapun. Agar mudah, kamu coba eliminasi variabel (y).
Eliminasi variabel tersebut dengan cara mengali dua persamaan yang ke-2. Maka, bentuk rumusnya adalah seperti berikut ini.
6x – 2y + 4z = 18 (persamaan 2)
x + 2y – z = 6 (persamaan 3)
Kemudian, kamu bisa tambahkan kedua persamaan tersebut.
Mengapa? karena -2y + 2y akan habis sehingga, kamu akan memperoleh persamaan linier dua variabel baru, yaitu:
7x + 3z = 24
Kamu sudah dapat dua persamaan linier dua variabel, yaitu
4x + z = 13, dan
7x + 3z = 24.
Setelah ini, kamu bisa melakukan konsep eliminasi kembali untuk memperoleh variabel (x), dan (z)
Ambil contoh penggunaan variabel (x). Setelah kamu hitung, kamu akan memperoleh nilai (x) adalah 3.
2. Metode Subtitusi
Ayo, coba kamu ingat-ingat lagi. Metode subtitusi juga sudah pernah kamu pakai untuk menyelesaikan konsep sistem persamaan linier dua variabel. Masih ingat?
Nah, metode subtitusi ini ternyata juga berlaku untuk menyelesaikan sistem persamaan linier tiga variabel.
Langsung saja, tadi kamu sudah dapat nilai x =3 saat melakukan metode eliminasi. Yuk, kembali ke persamaan linier dua variabel yang sudah kamu dapatkan. Misalnya, kamu pakai 4x + z = 13.
Kamu sudah tau kalau x = 3. Sekarang, kamu bisa mencari tahu nilai (z).
4x + z = 13.
4(3) + z = 13
12 + z = 13
z = 1
Nah, sekarang kamu sudah tahu kalau nilai x = 3, dan z = 1. Maka, yang perlu kamu lakukan setelahnya adalah mencari nilai (y).
Kembali ke soal awal sistem persamaan linear tiga variabel berikut:
x + y – z = 4 (persamaan 1)
3x – y + 2z = 9 (persamaan 2)
x + 2y – z = 6 (persamaan 3)
Ambil persamaan 1 saja karena bentuk persamaannya paling sederhana. Ingat, kamu sudah tahu nilai (x) dan (z). Sekarang kamu tinggal masukkan ke persamaannya
x + y – z = 4
3 + y – 1 = 4
2 + y = 4
y = 2
Jadi, nilai (x), (y), dan (z) pada persamaan linear tiga variabel berikut adalah (3, 2, 1). Himpunan penyelesaiannya bisa kamu tulis sebagai berikut:
Hp = { (3, 2, 1) }
Bagaimana, cukup panjang bukan? Meskipun terkesan panjang tapi, cara ini sebetulnya sangat sederhana dan bisa kamu pelajari pelan-pelan secara konsisten.
Apalagi, kalau kamu sudah menguasai sistem persamaan linier dua variabel, kamu akan cepat menguasai konsep sistem SPLTV ini.
Contoh Soal Persamaan Linear Tiga Variabel
Perhatikan contoh soal dan pembahasan tentangn SPLTV berikut ini dengan cermat supaya kamu bisa cepat memahami dan menguasai materi ini.
Soal
Temukan berapa nilai (x), (y), dan (z) pada persamaan berikut:
2x – y + z = 6 (persamaan 1)
x – 3y + z = -2 (persamaan 2)
x +2y – z = 3 (persamaan 2)
Pembahasan
Pertama, kamu pakai cara eliminasi. kamu akan ambil persamaan 1 dan 2.
2x – y + z = 6 (persamaan 1)
x – 3y + z = -2 (persamaan 2)
Kemudian, kurangi persamaan 1 dan 2 agar (z) habis. Maka, kamu akan mendapatkan persamaan dua variabel berikut.
x + 2y = 8 ….. (1)
Lalu, kamu ambil lagi persamaan 1 dan 3.
2x – y + z = 6 (persamaan 1)
x +2y – z = 3 (persamaan 3)
Jumlahkan persamaan 2 dan 3 agar (z) habis. Kemudian, kamu mendapatkan persamaan dua variabel berikut.
3x + y = 9 ….. (2)
Nah, sekarang kamu sudah punya x + 2y = 8 dan 3x + y = 9, kamu bisa mencari (x), atau pun (y) . Coba kamu cari (x), dengan mengkalikan dua persamaan linear dua variabel yang kedua.
x + 2y = 8
3x + y = 9 (x2) > 6x + 2y = 18
Kemudian, kamu bisa kurangi kedua variabel tersebut. Dengan begitu, kamu akan akan memperoleh hasil 5x = 10. Maka, x = 2.
Kemudian, karena x = 2, kamu juga akan mengetahui kalau y = 3. Nah, sekarang kamu tinggal mencari (z). Untuk memprosesnya, gunakan variabel pertama.
2x – y + z = 6
2(2) – 3 + z = 6
4 – 3 + z = 4
z = 5
Baca Juga : Pertidaksamaan Linear: Pengertian, Sistem, Bentuk Umum, Contoh
Yuk, Belajar Persamaan Linear Tiga Variabel!
Memahami sistem persamaan linear tiga variabel memang bisa terlihat menjemukan, tetapi konsep SPLTV ini dapat kamu terapkan dalam urusan-hitung menghitung di kehidupan nyata. Cara penyelesaiannya memang lebih panjang, tetapi efektif untuk kamu pelajari dan kuasai.