Dalam dunia statistik, median adalah jenis data yang harus Anda ketahui cara penghitungannya. Meski sudah banyak alat untuk membantu perhitungannya, namun tidak ada salahnya mempelajari cara menghitung median agar tidak lupa dengan dasar statistik. Berikut adalah langkah-langkah yang perlu Anda pahami!
Apa Itu Median, Mean, dan Modus?
Meski tujuan utama Anda adalah untuk mengetahui cara menghitung median, namun kurang lengkap rasanya jika tidak mengetahui dua jenis data lain dalam dunia statistik, yakni mean dan modus. Berikut adalah uraian penjelasannya:
1. Median
Median atau yang juga biasa disebut kuartil merupakan data statistik yang mewakili nilai tengah dari sekumpulan data. Sekumpulan data yang ingin dihitung sebelumnya harus sudah Anda uraikan dari data terkecil hingga terbesar atau sebaliknya.
Alasan mengapa data pada median harus berurutan adalah karena yang ingin Anda cari adalah nilai tengahnya. Selain itu, ada dua jenis median yang nanti dapat Anda pelajari di sub bab berikutnya.
2. Mean
Jika kata “mean” asing di telinga Anda, mungkin lain halnya dengan “rata-rata”. Kedua istilah ini memang memiliki arti yang sama. Agar dapat memperoleh mean, Anda dapat menjumlahkan semua nilai data yang tersedia pada suatu rentang dan membaginya dengan kuantitas data yang ada.
Jadi, mean adalah usaha pemusatan data untuk membagi suatu data menjadi setengah (50%) dari data terkecil dan terbesarnya. Selain mencari mean biasa, ada juga rumus untuk mencari mean kelompok.
3. Modus
Selain menjadi bahasa gaul, kata “modus” adalah kata yang juga sering muncul di dunia statistika. Berbicara mengenai hal yang sering muncul, mungkin sifat yang sama juga bisa Anda aplikasikan kepada cara menghitung modus. Modus sendiri merupakan sebutan untuk nilai yang paling sering muncul dari suatu kelompok data.
Berbeda cara menghitung median atau cara menghitung mean yang masih menggunakan rumus, modus sendiri hanya sekadar mengelompokkan data dan mengobservasinya saja. Nilai yang paling banyak ada di suatu rentang data dapat Anda katakan sebagai sebuah modus.
Jenis Median
Setelah tahu tiga rentang data yang sering digunakan dalam dunia statistika atau matematika pada umumnya, Anda dapat mempelajari tentang dua jenis median terlebih dulu. Nantinya, pemahaman ini akan berguna untuk memahami cara menghitung median yang baik dan benar. Berikut penjelasannya:
1. Median Data Tunggal
Sebuah median dapat Anda katakan sebagai median data tunggal jika datanya tidak terdapat dalam kelompok-kelompok tertentu. Jenis data ini bisa Anda temukan di nilai hasil ulangan atau tes dari sebuah kelas.
2. Median Data Kelompok
Median data kelompok merupakan sebuah angka yang bisa Anda dapat dengan mencari nilai tengah dari data menggunakan rentang kelompok tertentu. Biasanya, data seperti ini ditemukan pada sebuah sekumpulan data yang dikelompokkan dalam rentang data tertentu.
Sebagai contoh, warga kota Jakarta memiliki berat badan 40-44 kg, 45-49 kg, dst. Berbeda dengan median data tunggal yang mudah perhitungannya, mencari median data kelompok membutuhkan beberapa tahapan yang lebih rumit.
2 Cara Menghitung Median
Berikut adalah 2 cara yang dapat Anda gunakan jika ingin mencari median. Simak penjelasan lengkapnya:
1. Menghitung Median Data Tunggal
Pada perhitungan median data tunggal, Anda hanya perlu mengurutkan data dari yang paling kecil ke paling besar dan sebaliknya. Lalu, hitung jumlah data yang ada tersebut. Ingat! Hitung jumlah datanya, bukan jumlah nilainya.
Sebagai contoh, barisan data 1, 2, 3, 4, 5, 6, 7 memiliki jumlah data sebanyak 7 dengan jumlai nilai sebesar 28. Karena sudah Anda urutkan, maka median dari baris angka di atas adalah 4. Karena angka tersebut berada di tengah.
Beda halnya dengan barisan data 1, 2, 3, 4, 5, 6, 7, 8. Karena memiliki jumlah genap, maka tidak ada nilai tengah yang bisa Anda tentukan. Sehingga, Anda harus menjumlahkan data 4 dan 5, lalu bagi dua. Lewat perhitungan (4+5)/2, Anda akan mendapat nilai median sebesar 4,5.
2. Menghitung Median Data Kelompok
Seperti yang sudah dikatakan sebelumnya, cara menghitung median data kelompok agak berbeda ketimbang data tunggal. Agar dapat menyelesaikan data kelompok, Anda harus mengetahui beberapa istilah yang ada di rumus ini. Berikut penjelasanya:
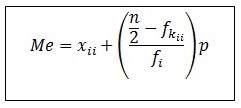
Me = Median yang ingin Anda cari.
xii = Batas median bawah yang bisa Anda cari dengan mengurangi batas bawah dengan 0,5.
N = jumlah data keseluruhan.
fkii = frekuensi kumulatif data sebelum kelas median.
fi = jumlah frekuensi atau banyak data pada rentang data di dalam kelas median.
p = rentang data dari sebuah kelas.
Supaya lebih jelas, Anda bisa melihat barisan data yang di bawah ini sebagai contoh soal:
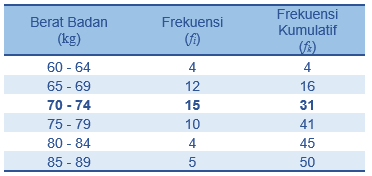
Lewat data tabel di atas, berapakah mediannya? Agar dapat mengetahui cara menghitung median data kelompok, pertama-tama Anda perlu mengidentifikasi komponen-komponen yang ada pada tabel di atas. Karena frekuensi kumulatif atau jumlah datanya adalah 50, maka n menjadi 50.
p dapat Anda lihat dari banyak data pada satu kelompok berat badan. Dalam tabel ini, terdapat angka 5. Lalu, untuk fi bisa Anda dapat angka 15. Sedangkan fkii adalah banyak data kumulatif sebelum kelompok data, yakni berjumlah 16.
Selanjutnya, untuk menghitung xii, Anda bisa melihat angka terkecil dari rentang data, yakni 70. Lalu, kurangkan dengan 0,5 menjadi 69,5. Setelah mendapat data-data di atas, Anda bisa menghitung median datanya dengan rumus median data kelompok, sebagai berikut:
Me = Xii + ((((n/2) – fkii) / fi ) p)
Me = 69,5 + ((((50/2) – 16) / 15) 5)
Me = 72,5
Setelah menggunakan rumus median data kelompok, Anda akan mendapat angka 72,5 sebagai hasilnya.
Sudah Paham Bagaimana Cara Menghitung Median?
Berikut tadi adalah serba-serbi tentang langkah menghitung median yang baik dan benar. Kini, Anda tidak perlu kebingungan jika harus mengerjakan soal yang berhubungan dengan median. Selamat berhitung!

