Operasi perkalian bilangan bulat menjadi salah satu materi wajib pada pelajaran matematika. Biasanya dasar-dasar perkalian sudah mulai dikenalkan pada siswa kelas 2 atau 3 Sekolah Dasar (SD). Materi ini juga merupakan konsep dasar dari operasi hitung sehingga para siswa harus menguasai dan memahami tentang perkalian.
Artikel ini akan memandu kamu memahami lebih baik konsep matematika yang satu ini!
Pengertian Bilangan Bulat
Apa itu bilangan bulat? Sederhananya, bilangan bulat merupakan kumpulan atau himpunan bilangan nilainya bulat atau yang tidak dalam bentuk pecahan atau desimal. Bilangan bulat juga sering disebut sebagai bilangan utuh yang terdiri dari bilangan positif, nol, dan bilangan negatif.
Baca Juga : Bilangan Bulat: Pengertian, Jenis, Urutan, dan Contoh Soal
3 Contoh Bilangan Bulat
Seperti penjelasan di atas, bilangan bulat terbagi menjadi tiga bagian yaitu bilangan asli, bilangan nol, dan bilangan bilangan negatif. Maka, himpunan bilangan bulat dapat dituliskan sebagai berikut: Z { …, -3, -2, -1, 0, 1, 2, 3, …}. Simak perinciannya pada contoh di bawah ini, yuk!

1. Bilangan Bulat Positif
Bilangan positif adalah bilangan asli yang memiliki nilai positif. Contoh dari bilangan bulat positif yaitu satu, dua, tiga, empat, dan lima (1, 2, 3, 4, dan 5). Dalam garis bilangan, bilangan bulat positif berada di sebelah kanan nol sehingga nilainya akan makin besar jika menjauh dari angka nol (0).
2. 0 (Nol)
Sedangkan angka nol (0) adalah bilangan bulat yang tidak memiliki nilai. Posisi angka nol (0) pada garis bilangan berada di tengah antara bilangan bulat positif dan negatif.
3. Bilangan Bulat Negatif
Jenis contoh bilangan bulat yang terakhir yaitu bilangan bulat negatif. Himpunan bilangan bulat negatif adalah minus lima, minus empat, minus tiga, minus dua, minus satu (…, -5, -4, -3, -2, -1, 0, …). Oleh karenanya, bilangan bulat negatif berada di sebelah kiri 0 pada garis bilangan.
Rumus Operasi Perkalian Bilangan Bulat
Pada dasarnya, operasi perkalian bilangan bulat adalah operasi yang melibatkan tanda perkalian (x). Perkalian juga dapat disebut sebagai penjumlahan yang berulang. Kamu perlu memahami setidaknya empat rumus rumus untuk operasi perkalian ini.
1. Perkalian Dua Bilangan Positif
Apabila bilangan bulat positif dikalikan dengan sesama bilangan bulat positif maka menghasilkan bilangan bulat positif. Jadi rumus dari perkalian dua bilangan positif yaitu:
a x b = ab
(+) x (+) = (+)
Contohnya adalah sebagai berikut:
- 3 x 3 = 9
- 4 x 3 = 12
- 5 x 6 = 30
- 6 x 7 = 42
Selanjutnya, cara penyelesaiannya adalah 5 x 6 = 5 + 5 + 5 + 5 + 5 + 5 = 30.
2. Perkalian Bilangan Bulat Positif dengan Negatif
Rumus untuk operasi perkalian bilangan bulat yang kedua berlaku apabila perkalian terjadi pada bilangan bulat positif dan negatif sehingga hasilnya akan negatif. Kondisi ini juga berlaku untuk sebaliknya.
a x (-b) = -ab
(+) x (-) = (-)
atau
(-a) x b = -ab
(-) x (+) = (-)
Contohnya adalah sebagai berikut:
- 3 x (-4) = – 12
- 3 x (-5) = -15
- (-6) x 2 = -12
- (-6) x 3 = -18
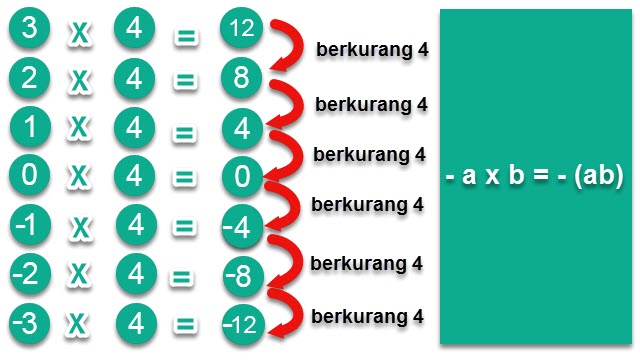
Pada contoh diatas, kita dapat menyimpulkan bahwa bilangan bulat positif jika dikalikan dengan bilangan bulat negatif dan sebaliknya maka selalu menghasilkan bilangan bulat negatif. Maka, jika dijabarkan menjadi seperti ini:
3 x (-4) = – (3 x 4) = – ( 3 + 3 + 3 + 3) = -12.
3. Perkalian Dua Bilangan Negatif
Selanjutnya, operasi perkalian antara dua bilangan bulat negatif hasilnya adalah bilangan bulat positif, sehingga setiap bilangan bulat (a) dan (b) selalu berlaku seperti di bawah ini:
(-a) x (-b) = ab
(-) x (-) = (+)
Contohnya adalah sebagai berikut:
- (-5) x (-5) = 25
- (-6) x (-6) = 36
- (-7) x (-2) = 14
- (-9) x (-2) = 18
Jika diuraikan maka menjadi:
(-5) x (-5) = – [(-5) + (-5) + (-5) + (-5) + (-5)] = -[25] = 25.
4. Perkalian Bilangan Bulat dengan 0 (Nol)
Sedangkan untuk perkalian bilangan bulat dengan 0, dapat dipahami melalui contoh di berikut:
- 3 x 0 = 0
- (-5) x 0 = 0
- 0 x (-9) = 0
- 0 x 1 = 0
Dari contoh diatas, sudah jelas bahwa semua bilangan bulat, baik itu bilangan bulat positif maupun negatif, jika dikalikan dengan nol (0) maka, hasilnya sudah pasti nol (0).
15 Contoh Soal Perkalian Bilangan Bulat dan Pembahasan
Setelah memahami rumus pada operasi perkalian bilangan bulat, saatnya berlatih dengan pemahaman dengan soal-soal berikut ini. Soal terdiri dari 10 pilihan ganda dan 5 esai. Siapkan kertas dan pensil untuk memulai latihan, ya!
Soal 1
3 x 9 = …
a. 27
b. 28
c. 26
d. 25
Jawaban: c. 27
Pembahasan
Perkalian bilangan positif dengan positif maka hasilnya adalah positif. Cara penyelesaiannya adalah 3 + 3 + 3 + 3 + 3 + 3 +3 +3 + 3 = 27.
Soal 2
Hasil dari operasi perkalian 12 x 5 = … adalah?
a. -60
b. 60
c. 17
d. -17
Jawaban: b. 60
Pembahasan
Perkalian dua bilangan positif selalu menghasilkan bilangan positif. Kemudian, cara penyelesaiannya adalah 12 x 5 = 12 + 12 + 12 + 12 + 12 = 60.
Soal 3
Hasil dari operasi perkalian 3 x (-5) = … adalah?
a. 5
b. 2
c. 15
d. -15
Jawaban: d. -15
Pembahasan
Hasil dari operasi perkalian bilangan bulat positif dan negatif adalah (-) negatif. Maka, hasil dari perkalian 3 x (-5) = – (3 x 5) = -15.
Soal 4
(-8) x (-5) = …
a. -40
b. 20
c. 40
d. -20
Jawaban: c. 40
Pembahasan
Perkalian sesama bilangan negatif akan menghasilkan bilangan positif, sehingga menjadi:
(-8) x (-5) = 8 x 5
= 40
Soal 5
(-7) x (-10) … 7 x 10
Tanda pembanding yang sesuai adalah?
a. <
b. >
c. =
d. ≥
Jawaban: c. =
Pembahasan
(-7) x (-10) = 70, sedangkan 7 x 10 = 70. Maka (-7) x (-10) dan 7 x 10 menghasilkan bilangan yang sama. Jadi tanda pembanding yang tepat adalah (=).
Soal 6
8 x 0 = …
a. 8
b. 1
c. 0
d. Tak terhingga
Jawaban: c. 0
Pembahasan
Perkalian bilangan bulat dengan 0 (Nol) akan selalu menghasilkan 0 (Nol). Jadi hasil dari 8 x 0 = 0.
Soal 7
Hitunglah operasi perkalian bilangan berikut ini:
11 x (-20) x 5 = …
a. 110
b. 1.100
c. -110
d. -1.100
Jawaban: d. -1.100
Pembahasan
Semua bilangan bulat positif apabila dikalikan dengan bilangan bulat negatif maka hasilnya adalah negatif, sehingga menjadi:
11 x (-20) x 5 = – (11 x 20 x 5)
= -1.100
Soal 8
6 x (-7) x 0 = …
a. 0
b. -32
c. 32
d. 1
Jawaban: a. 0
Pembahasan
Semua bilangan positif maupun negatif apabila dikalikan dengan 0 (Nol) maka hasilnya adalah tetap 0 (Nol)
Soal 9
Roni mengirim surat kepada 4 temannya. Dua surat memakai perangko seharga Rp 500 sedangkan dua surat lainnya memakai perangko seharga Rp 250. Maka, jumlah uang yang dikeluarkan untuk membeli perangko tersebut adalah …
Jawaban: 1500
Pembahasan
Roni membutuhkan 4 perangko dengan rincian sebagai berikut:
(2 x 500) + (2 x 250)
= 1.000 + 500
= 1.500
Soal 10
Di rumah Anisa terdapat 3 kamar tidur dan setiap kamar memiliki 2 jendela. Maka jumlah jendela di semua kamar tidur Anisa adalah …
Jawaban: 6
Pembahasan
Jumlah kamar di rumah Anisa yaitu 3 kamar sedangkan di setiap kamar masing masing memiliki 2 jendela.
Maka, operasi perkalian bilangan bulat yang dilakukan adalah 3 x 2 = 6.
Soal 11
Putri memiliki hobi mengumpulkan stiker. Ia dapat mengumpulkan 5 stiker setiap harinya. Maka, berapa jumlah pengumpulan stiker selama 10 hari?
Jawaban: 50 stiker
Pembahasan
Total stiker yang dikumpulkan setiap hari adalah 5. Kemudian dikalikan dengan pengumpulan selama 10 hari. Hasilnya adalah 5 x 10 = 50 stiker.
Soal 12
Berat badan Ian adalah 35 kg sedangkan berat Kasela 10 kg. Berapakah total berat badan Ian jika dikalikan dengan berat Kasela?
Jawaban: 350 kg
Pembahasan
Berat badan Ian apabila dikalikan dengan berat Kasela sehingga hasilnya adalah 35 x 10 = 35 + 35 + 35 + 35 + 35 + 35 + 35 + 35 + 35 + 35 = 350.
Soal 13
Dinda membeli 4 bungkus tempe. Masing-masing bungkus berisi 3 buah tempe. Berapa jumlah tempe yang Dinda beli?
Jawaban: 12 buah tempe
Pembahasan
Masing-masing bungkus berisikan 3 buah tempe dengan jumlah bungkus sebanyak 4. Jadi, operasi hitungnya yaitu 4 x 3 = 4 + 4 + 4 = 12.
Sudah Bisa Menghitung Perkalian Bilangan Bulat?
Secara garis besar, materi operasi perkalian bilangan bulat merupakan salah satu konsep perhitungan dasar dalam Matematika dan akan terus berkaitan dengan rumus Matematika lainnya. Oleh sebab itu, asah terus pemahaman dengan rajin berlatih agar kamu menguasai konsep ini dengan baik

